실전 예제 - 마케팅 데이터 분석 02 (Activation/Retention)

패스트캠퍼스 '직장인을 위한 파이썬 데이터분석 올인원 패키치 Online' 참조

 

 

 

 

01 Activation

• 지금까지 'Acquisition' 부분에서 세일즈가 어떻게 매체광고를 통해 영향을 받는지 알아 보았다.
• 다음 AARRR의 부분은 'Activation' 부분 이다. 이 부분에서는 Acquisition을 통해 매출을 올리고 그렇게 확보된 고객들을 계속해서 꾸준히 우리 제품에 'Active'하게 만드는 작업이다. 우리가 했던 매체광고를 예로 들면 고객들이 이 매체광고를 얼마나 자주 듣는지, 광고의 길이는 어떻게 되는지, 다음날에는 광고를 듣는지 등이 있다. 

 

 

 

02 Retention 문제 정의

• Acquisition → Activation 을 거쳤다면 이제는 그 고객들을 계속해서 유지하는 단계가 필요하다. 즉 고객들이 우리 서비스에 얼마나 유지가 되는지를 보는 것.
• 실습을 통해 이 Retention 작업을 해 보자.  모바일 게임 데이터로 A/B 테스트를 통해 Retention을 비교 할 예정. 

* 필수 라이브러리

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

df = pd.read_csv('cookie_cats.csv')
df.head()

1. sum_gamerounds - 첫 설치 후 14일 간 유저가 플레이한 라운드 수
2. retention_1 - 유저가 설치 후 1일 이내에 다시 돌아왔는지 여부
3. retention_7 - 유저가 설치 후 7일 이내에 다시 돌아왔는지 여부

 

▶ 이 게임의 특성을 알 필요가 있다. 

• 이 게임의 경우 특정 스테이지가 되면 스테이지가 잠기는데 이때 이 스테이지를 열려면 키를 3개 구하거나, 페이스북 친구에게 요청하거나, 유료로 결제를 해야 한다.
• 이때 스테이지를 몇번째에 잠궈야 이용자 Retention이 가장 좋을지 결정 해야 한다. 

 

 

 

03 EDA

df.shape
(90189, 5)

df.isnull().sum()
userid            0
version           0
sum_gamerounds    0
retention_1       0
retention_7       0

# A/B 테스트로 사용된 버전별로 유저들은 몇명씩 있는지 체크
df.groupby('version').count()

# 유저 플레이 라운드 수를 시각화 해서 보자
sns.boxenplot(data=df, y='sum_gamerounds')

• 대부분의 유저가 밑에 10000판 이하로 몰려있는데 몇몇의 유저들이 50000판 가까이에 몰려있다. 아웃라이어가 분명하다

# 아웃 라이어 체크 후 제거
df[df['sum_gamerounds'] > 45000]

# 아웃라이어 제거
df = df[df['sum_gamerounds'] < 45000]
print(df.shape)
(90188, 5)

50000판 가까이 한 유저는 단 1명!

 

# 상위 50% 유저들의 플레이 횟수 체크
df['sum_gamerounds'].describe()
count    90188.000000
mean        51.320253
std        102.682719
min          0.000000
25%          5.000000
50%         16.000000
75%         51.000000
max       2961.000000

• 90188 명 중 대부분은 51판 정도 플레이 했고 표준편차는 조금 다소 높게 나왔다.
• 상위 50% 이상 유저들은 보통 16판 정도 한것으로 나왔다. 

# 다시 시각화로 체크
sns.boxenplot(data=df, y='sum_gamerounds')

아웃라이어만 제거해도 이렇게 데이터를 볼 수 있다

 

 

 

 

04 데이터 분석

# 각 게임실행횟수 별 유저의 수를 카운트 해봅니다
plot_df = df.groupby('sum_gamerounds')['userid'].count() # 게임라운드를 유저 아이디 별로 그룹화
plot_df
sum_gamerounds
0       3994
1       5538
2       4606
3       3958
4       3629
        ... 
2251       1
2294       1
2438       1
2640       1
2961       1



# 시각화로 파악
ax = plot_df[:100].plot(figsize=(10,6))
ax.set_title('The number of players that played 0-100 game roungs during the first week')
ax.set_ylabel('Number of players')
ax.set_xlabel('# Game rounds');

• 게임을 설치하고도 한 번도 실행하지 않은 유저들의 수가 꽤 되는 것을 알 수 있다 (설치만 한 4000명가까이 되는것으로 보인다)
• 몇몇 유저들은 설치 첫주에 충분히 실행을 해보고 다시 게임을 또 하게 되는것도 볼 수 있다.
• 비디오 게임 산업 뿐만 아니라 모든 산업이 1-day retention이 얼마나 중요한 평가 지표인지 알 수 있다.
• 즉 1-day retention이 높을 수 록 손쉽게 가입자 기반을 유지 할 수 있다.

 

- retention을 기반으로 분석

# 1-day retention 평균
df['retention_1'].mean() #True/False로 나뉘기때문에 0,1로 구분
0.4452144409455803

# 그룹에 따른 1-day retention 비교
df.groupby('version')['retention_1'].mean() #그룹을 버전으로 묶으면서 버전마다 retention_1의 평균을 가져옴
version
gate_30    0.448198
gate_40    0.442283

# 7-day retention도 확인
df['retention_7'].mean()
0.1860557945624695

# 그룹에 따른 1-day retention 비교
df.groupby('version')['retention_7'].mean() #그룹을 버전으로 묶으면서 버전마다 retention_1의 평균을 가져옴
version
gate_30    0.190183
gate_40    0.182000

• 단순 그룹별 비교시에는 게이트 게이트 30이 미세하게 플레이 횟수가 더 많다
• 이 작은 차이가 나중에는 고객의 retention과 수익에 직결 될 것
• 7일로 비교해도 게이트 30이 미세하게 더 높음. 1일때보다 7일때 훨씬 더 retention 비율이 높게 나왔다
• 그렇다면 게이트를 30에 잠그는게 더 효과적인가를 깊게 들여다 봐야 한다.

 

▶ 데이터를 검증 하자!

• 두 그룹의 차이가 나오긴 했으나 이것이 정말 유의미 한지 검증을 해야 한다.
• 연속형 데이터에서 검증 방법은 여러가지가 있으나 크게 부트스트랩/t-검증/카이 스퀘어를 통해 검증을 할 예정

 

부트스트랩(Bootstrap) - 모수의 분포를 추정하는 강력한 방법중 하나는 표본에서 추가적으로 표본을 복원 추출하고 각 표본에 대한 통계량을 다시 계산하는것이다. 이러한 절차를 부트스트랩이라 한다. 부트스트랩의 과정은 다음과 같다 
1) 1억개의 모집단에서 200개 표본 추출
2) 200개의 표본 중 하나를 뽑아 기록 후 제자리에 둠
3) 이를 n번 반복
4) n번 재표본추출한 값의 평균을 구함
5) 2~4단계를 r번 반복 (r:부트스트랩 반복 횟수)
6) 평균에 대한 결과 r개를 사용하여 신뢰구간을 세팅
7) r이 클수록 신뢰구간에 대한 추정은 더 정확해짐

 

* 신뢰구간이란?
모수가 어느 범위 안에 있는지를 확률적으로 보여주는 방법. 95%의 신뢰구간이라고 불리며 확률표본을 뽑았을때 95%가 이 구간에 있을거라고 확신 할 수 있는 구간

 

# 각각의 AB그룹에 대해 bootstrap된 means 값의 리스트를 만듬
# 하나씩 뽑아서 mean값을 넣어주는 행위
boot_1d =[]
for i in range(1000):
    boot_mean = df.sample(frac=1, replace=True).groupby('version')['retention_1'].mean()
    boot_1d.append(boot_mean) # retnetion_1의 대한 평균값들이 들어감
    
# 받은 리스트를 DF로 변환
boot_1d = pd.DataFrame(boot_1d)

# 부트스트랩 분포에 대한 Kernel Density Estimate plot
boot_1d.plot(kind='density');

• gate_40은 0.440 언저리, gate_30은 0.458 언저리 즉 이 두 평균 사이의 차이가 두 집단 간의 retention_1의 평균 차이를 나타냄
• 위의 두 분포는 A/B 두 그룹에 대해 1-day retention이 가질 수 있는 부트스트랩의 불확실성을 표현하고 있음. 그 뜻은 두 표본집단이 같은 모집단에서 나왔을 가능성이 있고 두 표본집단의 차이가 통계적으로 유의하지 않을 수 있다는 말
• 두 그룹의 평균 차이가 작지만 이를 자세히 보기 위해 %차이를 시각화 해봐야 한다

# 두 AB 그룹간의 %차이 평균 컬럼을 추가
boot_1d['diff'] = (boot_1d.gate_30 - boot_1d.gate_40)/boot_1d.gate_40 * 100

# %차이를 시각화
ax = boot_1d['diff'].plot(kind='density')
ax.set_title('% difference in 1-day retention between the two AB-groups')

# 게이트가 30에 잠길때 1-day retention이 클 확률 계산
print('게이트가 레벨 30에 잠길 때 1-day retention이 클 확률:',(boot_1d['diff'] > 0).mean())

• 비율 계산식이 들어가도록 하여 % 차이를 출력 - 예로 a,b의 키가 170, 175일때 둘의 차이는 5cm인데 둘의 차이를 퍼센트 비율로 보려면 (175-170)/170*100을 해야 5cm가 퍼센트로 떨어지게됨
  즉 30수치 - 40 수치 / 40 수치 * 100 하면 두 그룹간의 차이의 %가 나옴
  계산시에 무얼로 나누는지는 큰 상관 없음.
• 비율 관련 링크 (https://zxchsr.tistory.com/113)

• 그래프를 해석하면 가장 가능성이 높은 % 차이는 약 1~2%이며 분포의 95%는 0% 이상이라는것을 그래프 상에서 볼 수 있고 레벨 30에 게이트를 락을 걸기를 추천 한다라고 보인다.
• 다시 말해 게이트가 레벨 30에서 잠길때 1일 유지율이 더 높을 가능성이 있다라고 말해 주고 있음
• 여기서 중요 포인트는 레벨 30에 게이트의 락을 걸면 1일 유지율은 높아진다 하지만 다른 유저들은 아직 레벨 30에 다다르지 않았을 가능성도 크고 이에 따라 retention영향을 받지 않을 수 도 있다.
• 더욱이 7일 이후에는 더 많은 플레이어들이 레벨 30/40에 도달하기때문에 7일의 retention 비율도 확인해야함

 

- 7일 데이터 분석

# 7일 비율 확인
df.groupby('version')['retention_7'].sum() / df.groupby('version')['retention_7'].count()
version
gate_30    0.190183
gate_40    0.182000

• 1일과 마찬가지로 게이트 30이 근소하게 앞서고 1일때보다도 퍼센트 차이가 확실함. 이 유이는 아마 더 많은 플레이어들이 1일보다 더 많이 플레이를 하면서 첫 번째 게이트를 열어볼 시간이 있었기 때문이라고 볼 수 있음
• 7일 retention비율은 1일때보다 낮음. 기 이유는 설치 후 하루보다 일주일 후에 게임을 하는사람이 당연히 더 적을것이기 때문
• 이전과 마찬가지로 7일 데이터도 부트스트랩으로 AB간의 그룹차이가 있는지 분석을 해야함

# 7일 RETENTION 부트스트랩
# 각각의 AB그룹에 대해 bootstrap된 means 값의 리스트를 만듬
# 하나씩 뽑아서 mean값을 넣어주는 행위
boot_7d =[]
for i in range(500):
    boot_mean = df.sample(frac=1, replace=True).groupby('version')['retention_7'].mean()
    boot_7d.append(boot_mean)
    
# 받은 리스트를 DF로 변환
boot_7d = pd.DataFrame(boot_7d)

# 두 AB 그룹간의 %차이 평균 컬럼을 추가
boot_7d['diff'] = (boot_7d.gate_30 - boot_7d.gate_40)/boot_7d.gate_40 * 100

# %차이를 시각화
ax = boot_7d['diff'].plot(kind='density')
ax.set_title('% difference in 1-day retention between the two AB-groups')

# 게이트가 30에 잠길때 7-day retention이 클 확률 계산
print('게이트가 레벨 30에 잠길 때 7-day retention이 클 확률:',(boot_7d['diff'] > 0).mean())

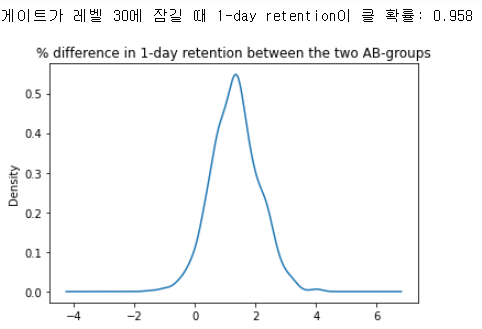
• 위에서 게이트 30/40 의 retention 차이는 극소하게 났었고 이게 정말 차이가 있는지를 봤어야 했다. 확실히 레벨 30에 게이트를 잠궈야 retention의 확률이 1에 가깝게 나온다는것을 알 수 있다. 

 

 

05 통계적 비교

• 단순히 그룹간 평균을 비교해서 게이트40(44.2%)이 30(44.8%)보다 플레이 횟수가 더 적다는것을 알 수 있다
• 작은 차이이지만 이 작은 차이가 retention 비율, 더 나아가 장기적 수익에도 더 영향을 미치게 될 것
• 그런데 이것만으로 30게이트가 확실히 낫다라고 확신 할 수 있을까? 이때 사용하는것이 통계적 비교(t_test)

* t-test란?

• t-검정으로 불리며 표본으로 부터 추정된 분산이나 표준편차를 가지고 검정하는 방법으로 '두 집단에 차이가 있는지 없는지'를 판단하는 기준이 됨
• t테스트를 통해 나오는 수치가 유의확률 0.05보다 작으면 평균 차이가 유의미한 것으로 해석되어 귀무가설을 기각. 그 반대의 경우, 평균 차이가 유의미하지 않으므로 귀무가설을 수용
  (참조 링크:https://m.blog.naver.com/sendmethere/221333164258)

# t-test 진행
from scipy import stats

tTestResult = stats.ttest_ind(df_30['retention_1'], df_40['retention_1'])
tTestResultDiffVar = stats.ttest_ind(df_30['retention_1'], df_40['retention_1'], equal_var=False)

tTestResult
Ttest_indResult(statistic=1.7871153372992439, pvalue=0.07392220630182522)

tTestResult = stats.ttest_ind(df_30['retention_7'], df_40['retention_7'])
tTestResultDiffVar = stats.ttest_ind(df_30['retention_7'], df_40['retention_7'], equal_var=False)

tTestResult
Ttest_indResult(statistic=3.1575495965685936, pvalue=0.0015915357297854773)

• p-value는 0.05이하로 나와야 유의미하다고 판단 할 수 있음. 
• 결과를 보면 1일차만 가지고는 게이트를 어디에 락을 걸지는 판단하기 힘들지만 7일차 혹은 그 이상으로 갈수록 차이가 확실해진다고 나와있는것. 즉 7일차 기준으로 게이트 30에 락을 걸어야 고객들의 retention 비율이 올라가게되고 장기적으로 매출에도 영향이 있을것으로 보임

 

• 사실 retention_7은 수치형이아닌 불린형으로 t-test검정과는 맞지 않음. 범주형을 검증할때는 'chi-square'가 적절함

* chi-square란?

• 어떤 범주형 확률변수 x가 다른 범주형 확률변수 y와 독립인지 또는 상관관계를 가지는지 검증하는데 사용
• 카이제곱검정을 독립을 확인하는데 사용하면 카이제곱 독립검정으라고 부름
• 만약 두 확률변수가 독립이라면 x=0 일때 y분포와 x=1일때 y분포가 같아야 함. 게이터 버전에 관계없이 y의 분포가 같다는말. 즉 카이제곱검정이 맞다면(채택된다면) 두 확률 변수는 독립이고 기각된다면 두 확률변수는 상관관계가 있다고 볼 수 있음
• 다시말해 카이제곱검정결과가 기각된다면 게이트가 30/40에 따라 retention비율이 변화하게될것임
• x의 값에 따른 각각의 y분포가 2차원표의 형태로 주어지면 독립된 경우의 분포와 실제 y표본분포의 차이를 검정통계량으로 계산하게 됨. 이 값이 충분히 크다면 x와y는 상관관계가 있다고 봄

# 카이제곱검정을 위한 분할표 생성
# 버전별로 생존자의 수 합계를 구함
df.groupby('version').sum()

# 버전별 전체 유저의 수
df.groupby('version').count()

▶ 분할표를 가지고 카이검정제곱을 진행

# 버전별 분할표
import scipy as sp
obs1 = np.array([[20119, (45489-20119)], [20034, (44699-20034)]])
sp.stats.chi2_contingency(obs1)

(3.1698355431707994,
 0.07500999897705699,
 1,
 array([[20252.35970417, 25236.64029583],
        [19900.64029583, 24798.35970417]]))

• 1-day retention에서 30/40의 유의확률은 7.5%로 상관관계가 있다고 말 할 수 없음

obs7 = np.array([[8501, (44699-8501)], [8279, (45489-8279)]])
sp.stats.chi2_contingency(obs7)
(9.915275528905669,
 0.0016391259678654423,
 1,
 array([[ 8316.50796115, 36382.49203885],
        [ 8463.49203885, 37025.50796115]]))

• 7-day retention의 경우 0.001로 유의확률 0.05%보다 낮으므로 x와y는 상관관계가 있다고 말 할 수 있음
• 쉽게 말해 게이트 위치에 따라 유저 retention 비율에 차이가 있다는 말
• 정리하자면 맨 처음 30/40에 차이가 아주 미세하게 났고 1일과 7일차이에도 차이가 있으나 미세했다. 이거를 지금까지 t-test/카이제곱 검정으로 검정한 결과 미세하게 차이가 나도 확실히 게이트를 어디에 두느냐에 따라 유저 retention 비율이 달라지고 장기적으로는 매출에까지 영향이 갈 것이라고 판단이 된다고 할 수 있음

 

 

 

 

06 테스트 결과 적용 방안

• 수치형이냐 범주형이냐에따라 테스트 방안은 달라진다 (t-test vs 카이제곱검정)
• 둘다 p-value를 중점으로 봐야하고 p-value가 0.05보다 작으면 A/B테스트가 유의미하다고 볼 수 있음
  (예: 게이트 30 VS 40 중 어디에 락을 걸어야 유저수가 더 잘 유지 되냐 → A/B 테스트)
• 결론으로 게이트 30에 락을 걸어야 함
• 더 생각해봐야 할 문제들
  Retention 비율 포함하여 여러 고려해야할 다양한 메트릭들이 있음. 
  종사하는 분야에 따라 어떤 메트릭을 가지고 그 기준으로 테스트 하고 결과를 볼건지 정하는게 중요!