실전 예제 - 시계열 분석 13

패스트캠퍼스 '직장인을 위한 파이썬 데이터분석 올인원 패키치 Online' 참조

 

 

 

 

 

 

 

 

01 데이터 안정성 보장의 필요성

• 시계열 분석을 하다보면 시계열 모델은 'Stationary(변동이 없는)' 하다라는 말을 많이 듣는다. 즉 변동이 없고 시계열 데이터가 미래에 똑같은 모양일 확률이 매우 높다는 말이다.
• 즉 시계열이 안정적이지 않으면 현재의 패턴이 미래에 똑같이 재현되지 않으므로 안정적인 시계열을 써야 한다. 

• 시계열의 안정성을 판별하는 방법은 '(Augmented) Dickey Fuller Test'라는 방법이 있다. 원 귀무가설은 원 계열은 안정적이지 않다라고 가정하에 시작한다. 예로 주가는 항상 올라갔다가 내려갔다가 안정적이지 않다는 것.

 

 

 

 

02 주기에 따른 특성

• 전시간에는 트렌드와 계절에 따른 요인을 분리하고 분석했다. 
• 이번에는 주기에 따른 특성을 분석 및 안정성에 대해 공부 예정

 

• 미국의 FRED라는 데이터를 제공해주는 웹사이트에서 환율 데이터를 받음

# 필수 라이브러리 및 데이터 다운

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from statsmodels.tsa.stattools import adfuller

df=pd.read_csv('https://raw.githubusercontent.com/sm-joo/sm-joo/master/DEXKOUS.csv', parse_dates=['DATE'], index_col='DATE')
df.head()

• 똑같이 날짜부분을 인덱싱으로 보냄과 동시에 Date형태로 바꿔 준다

▶ 데이터 간단 정리

# 데이터 확인
df.info()
 #   Column   Non-Null Count  Dtype 
---  ------   --------------  ----- 
 0   DEXKOUS  1306 non-null   object
 
 # 컬럼 이름 짧게 변경
df.columns = ['KOUS']

df['KOUS'].replace('.','',inplace=True)

df['KOUS'] = pd.to_numeric(df['KOUS'])

df.info()
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   KOUS    1251 non-null   float64
 
 
 # 결측치 확인
df.isnull().sum()
KOUS    55

# 결측치 처리
df['KOUS'].fillna(method='ffill', inplace=True)
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   KOUS    1306 non-null   float64

▶ 시각화로 파악

df['KOUS'].plot(figsize=(10,6));

환율이 왔다갔다 하는것을 볼 수 있다.

 

▶ '.resample()' / '.rolling()'

# .resample() -> 일별 데이터를 주,월 단위로 변환 가능
# df.resample('W-Fri').last() -> 구체적으로 주 단위로 들고 와짐
# df.resample('M').last()
df.resample('W-Fri').last().plot(figsize=(15,6))

# .rolling() -> 이전 xx일에 대한 이동 평균, 이동 sum을 산출 할 수 있음
df.rolling(10).mean().head(20) # 이전 30일에 대한 값

• 이전 10일에 대한 평균을 뽑아오는데 맨 앞 10개를 거르고 뽑힘
• 맨 처음 그래프를 보면 정확히 보기 힘들기 때문에 원 데이터를 이 두개의 함수로 쉽게 바꿔서 볼 수 있다.

# 매 월의 표준 편차
df.rolling(30).std().resample('M').mean().plot()

 

• 16~17년도의 환율 변동폭이 크고 18년 말부터 환동 폭이 작다 

 

 

 

03 안정성 테스트

adfuller(df['KOUS'])

 

• 두번째 값이 'p-value'이다. 0.08이므로 0.05를 넘어간다. 데이터가 안정적이지 않다는 말
• 변환하는 방법 3가지는 아래와 같다. 

# 안정성 있게 변하는 공식은 아래와 같다
# y(t+1)/y(t) - 1 -> 증가율
# log(y(t+1))-log(y(t)) -> 로그 차분

adfuller(df.KOUS.pct_change().dropna())
(-26.943541201332884,
 0.0,
 1,
 1303,
 {'1%': -3.435378572037035,
  '5%': -2.863760700696655,
  '10%': -2.56795231450063},
 -9698.633396210715)
 
(df.KOUS/df.KOUS.shift(1)-1).dropna()
2015-03-16   -0.005354
2015-03-17   -0.001709
2015-03-18   -0.000532
2015-03-19   -0.005217
2015-03-20   -0.006546
                ...   

(np.log(df.KOUS)-np.log(df.KOUS.shift(1))).dropna()
2015-03-16   -0.005368
2015-03-17   -0.001710
2015-03-18   -0.000532
2015-03-19   -0.005231
2015-03-20   -0.006568
                ...

 

 

 

04 시계열의 두가지 유형

• 시계열의 근간을 이루는 유형이 2가지가 있다. AR/MA
• AR - 자기회귀모델 → 과거가 미래를 예측한다. (직관적인 사실에 의존)

• 이전기의 실적으로 계산이 되어지기때문에 자귀회귀모델이라고 불려지고 et가 점점 1에서 멀어질수록 실적이 떨어지게 됨
• MA - 이동평균모델 → 과거의 시계열 값 대신 과거의 오차를 이용해 예측

 

 

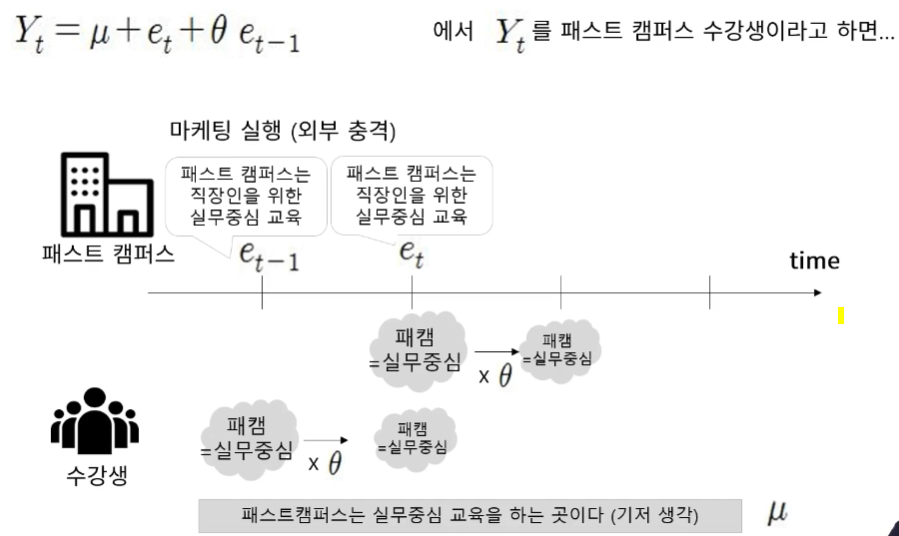
▶ AR/MA 모델 판별 방법

• ACF(Auto Correlation Function) / PACF(Partial Auto Correlation Function) 두가지 방법이 있음

- 이를 쉽게 예로 들면

ACF의 경우 모든 상관관계를 다 계산하게되므로 천천히 줄어들고 PACF같은 경우는 직접적으로 관련이 있는 관게만 계산하므로 하나만 튀고 뒤로 갈수록 의미가 없어짐

결론적으로 PACF는 AR/MA든 둘다 직접적 데이터만 쓰기에 하나만 튀어올라왔다가 교대로 줄어들게 되고 ACF같은 모든 데이터를 통해 계산하기 때문에 서서히 줄어드는 모양새를 보임. AFC해석 그래프를 보면 마케팅효과를 줬을때 다음때에 얼마나 남아있나를 보여주는데 점점 줄어드는것을 볼 수 있다.

 

 

 

05 ACF / PACF 실습

• 외부 요인이 얼마나 지속되는지를 검토 해보자 → 마케팅 활동 효과가 몇주간 지속되는지? / 이번주 진행한 마케팅 활동이 얼마나 지속되는지?

# 필수 라이브러리

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 전시간 전처리 했던 데이터로 진행
df=pd.read_csv('https://raw.githubusercontent.com/sm-joo/sm-joo/master/DEXKOUS.csv', parse_dates=['DATE'], index_col='DATE')
df.columns=["KOUS"]
df['KOUS'].replace('.', '', inplace=True)
df['KOUS'] = pd.to_numeric(df['KOUS'])
df.fillna(method='ffill', inplace=True)

df.plot(figsize=(16,5));

2017년에는 안정적인 환율성을 보이고 2019년부터 다시 불안정함을 보인다. 이 두개의 년도로 실습!

 

 

▶ 전처리

# 주단위로 변환
df_w = df.resample('W-Fri').last()
df_w.head()

# 2017년도와 2019년도 구별
df_2017 = df_w[df_w.index.year==2017]
df_2019 = df_w[df_w.index.year==2019]

df_2017.plot();
df_2019.plot();

# AutoCorrelation 그래프
plot_acf(df_2017);

plot_acf(df_2019);

• AutoCorrelation 으로 외부의 충격이 얼마나 지속되냐를 볼 수 있는데 2017년은 첫 충격 이후 바로 0.75로 떨어지면서 3주까지 지속됬고 2019년에는 17년도보다는 완만하게 떨어지고 4주간 지속 된것을 볼 수 있다

▶ ACF/PACF 비교

# 첫번째 행 : 2017년 데이터의 원계열, ACF, PACF
# 두번째 행 : 2019년 데이터의 원계열, ACF, PACF 
figure, axes = plt.subplots(2, 3, figsize=(16, 7)) # 6개의 파레트 하나씩 채움
axes[0,0].plot(df_2017)
axes[0,0].set_title('Original Series(2017)')
axes[1,0].plot(df_2019)
axes[1,0].set_title('Original Series(2019)')
plot_acf(df_2017, ax=axes[0,1])
plot_acf(df_2019, ax=axes[1,1])
plot_pacf(df_2017, ax=axes[0,2])
plot_pacf(df_2019, ax=axes[1,2]);

• 19년도가 17년도에 비해 외부 충격이 오래 지속되었다 3-4주.
• 17년에는 외부 충격이 다음기에 0.75남았지만 19년도에는 0.9가 남아있다. 즉 Persistency가 증가 하고 있다.
• 가입자, 사용자 마케팅 효과 분석에 활용
• 주가지수, 환율이 외부 충격에 얼마나 오래 지속되는가