머신러닝 06 - sklearn 알아 보기 (비지도 학습)
패스트캠퍼스 '직장인을 위한 파이썬 데이터분석 올인원 패키치 Online' 참조
01 비지도 학습이란?
- 기계 학습의 일종으로 데이터가 어떻게 구성되었는지를 알아내는 문제의 범주에 속한다. 이 방법은 지도학습 혹은 강화학습과 달리 입력값에 대한 목표치가 주어지지 않는다
- 방법으로는 차원축소, 군집화가 있다
02 차원축소
- feature의 개수를 줄이는 것을 넘어 특징을 추출하는 역할
- PCA, LDA, SVD 로 나뉨
- 계산 비용을 절감하고 전반적인 데이터에 대한 이해도를 높이는 효과
▶ PCA
- 주성분 분석(PCA)는 선형 차원 축소 기법이다. 매우 인기 있게 사용되는 차원 축소 기법 중 하나.
- 주요 특징중 하나는 분산(variance)을 최대한 보존 한다는 점
- 참조 블로그 (https://excelsior-cjh.tistory.com/167)

- 세팅시에 n_components에 1 > 면 분산을 기준으로 차원 축소, 1 < 면 해당 값을 기준으로 feature를 축소함
* 데이터 세팅
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import datasets
import pandas as pd
iris = datasets.load_iris()
data = iris['data']
df = pd.DataFrame(data, columns=iris['feature_names'])
df['target'] = iris['target']
pca = PCA(n_components=2)
# PCA전에 스탠다드스캐일러로 스캐일을 평균 0, 표준편차를1로 만들어야함
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)':'petal width (cm)'])
pca_data = pca.fit_transform(data_scaled)
pca_data[:5] #차원을 2개로 축소했기때문에 한 값에 2값만 나옴
array([[-2.26470281, 0.4800266 ],
[-2.08096115, -0.67413356],
[-2.36422905, -0.34190802],
[-2.29938422, -0.59739451],
[-2.38984217, 0.64683538]])- 시각화로 확인
import matplotlib.pyplot as plt
from matplotlib import cm
import seaborn as sns
%matplotlib inline
plt.scatter(pca_data[:, 0], pca_data[:, 1], c=df['target']) [행 인덱스, 열 인덱스]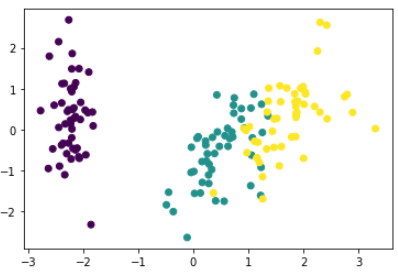
- 1보다 낮게하여 분산 기준으로 축소
# components > 1 하여 분산 기준으로 축소
pca = PCA(n_components=0.99)
pca_data = pca.fit_transform(data_scaled)
pca_data[:5] # 분산기준으로하면 컬럼이 몇개나올지는 랜덤임
array([[-2.26470281, 0.4800266 , -0.12770602],
[-2.08096115, -0.67413356, -0.23460885],
[-2.36422905, -0.34190802, 0.04420148],
[-2.29938422, -0.59739451, 0.09129011],
[-2.38984217, 0.64683538, 0.0157382 ]])- 3D로 확인
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection='3d') # Axe3D object
sample_size = 50
ax.scatter(pca_data[:, 0], pca_data[:, 1], pca_data[:, 2], alpha=0.6, c=df['target'])
plt.savefig('./tmp.svg')
plt.title("ax.plot")
plt.show()
▶ LDA
- 'Linear Discriminant Analysis'로 선형 판별 분석법으로 불린다
- PCA와 비슷함. 클래스 분리를 최대화 하는 축을 찾기 위해 클래스 간 분산과 내부 분산의 비율을 최대화 하는 방식으로 차원을 축소함
- PCA는 분산을 최대한 유지하는 반면, LDA는 각각의 고유 레이블이나 클래스간의 분리를 최대한 하기위해 노력함
# LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
lda = LinearDiscriminantAnalysis(n_components = 2)
#스탠다드스캐일러로 스캐일을 평균 0, 표준편차를1로 만들어야함
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)':'petal width (cm)'])
lda_data = lda.fit_transform(data_scaled, df['target'])
lda_data[:5]
array([[ 8.06179978, 0.30042062],
[ 7.12868772, -0.78666043],
[ 7.48982797, -0.26538449],
[ 6.81320057, -0.67063107],
[ 8.13230933, 0.51446253]])- 시각화
plt.scatter(lda_data[:, 0], lda_data[:, 1], c=df['target'])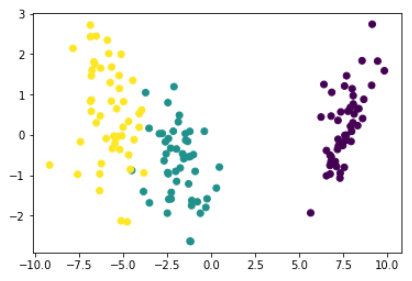

▶ SVD
- 'Singular Value Decomposition' 으로 상품의 추천 시스템에도 활용되어지는 알고리즘 (추천시스템)
- 특이값 분해 기법. PCA와 유사한 차원 축소 기법. scikit-learn 패키지에서는 'truncated SVD (aka LSA)'를 사용함
from sklearn.decomposition import TruncatedSVD
# 스탠다드스캐일러로 스캐일을 평균 0, 표준편차를1로 만들어야함
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)':'petal width (cm)'])
svd = TruncatedSVD(n_components=2)
svd_data = svd.fit_transform(data_scaled, df['target'])
plt.scatter(svd_data[:, 0], svd_data[:, 1], c=df['target'])
03 군집화
- 클러스터링으로 불리며 X값을 주면 스스로 분류를 하게 된다.
- K-Means/DBSCAN 으로 나뉜다
▶ K-Means
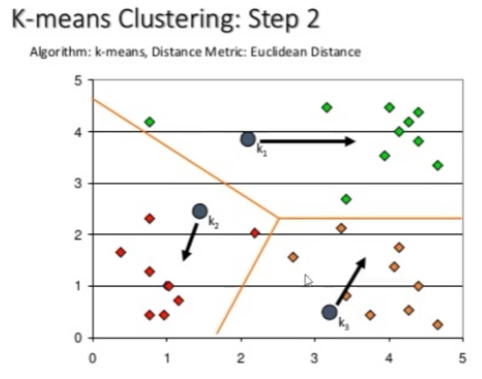
- 중심 데이터를 찾은 후 점을 찍고 거기서 가까운 점을 찾고 거기서 다시 중간 점을 찾고 계속해서 중간 점을 찾아가면서 값을 분류 함
- 주로 스팸 문자 분류, 뉴스 기사 분류등에 쓰인다.
- 하이퍼파라미터 중 'max_iter'를 조절하여 군집 분포를 조절 할 수 있다.
# K-Means
from sklearn.cluster import KMeans
#몇개의 그룹인지 모를때는 군집수를 여러번 돌려봐야함
kmeans = KMeans(n_clusters=3)
cluster_data = kmeans.fit_transform(df.loc[:, 'sepal length (cm)':'petal width (cm)'])
cluster_data[:5]
array([[3.41925061, 0.14135063, 5.0595416 ],
[3.39857426, 0.44763825, 5.11494335],
[3.56935666, 0.4171091 , 5.27935534],
[3.42240962, 0.52533799, 5.15358977],
[3.46726403, 0.18862662, 5.10433388]])
kmeans.labels_
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2,
2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 2, 2, 2, 2,
2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0])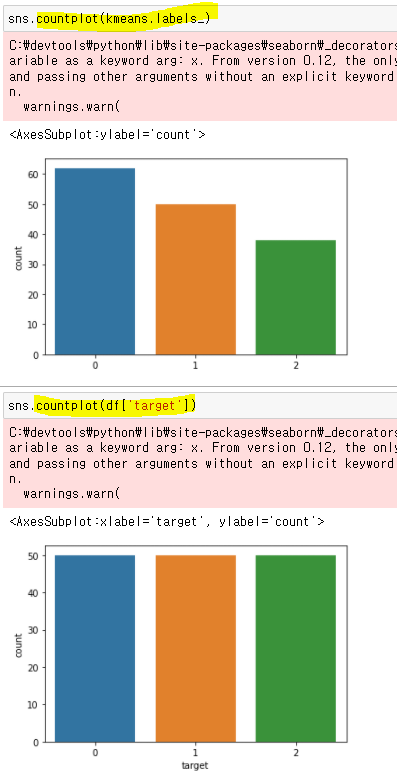
▶ DBSCAN (Density-based spatial clustering of applications with noise)
- 밀도가 높은 부분을 클러스터링 하는 방식
- 어느점을 기준으로 반경 x내에 점이 n개 이상 있으면 하나의 군집으로 인식하는 방식
- DBSCAN은 n_cluster 지정 필요 없음
- 기하학적인 clustering도 잘 찾아냄

from sklearn.cluster import DBSCAN
# DBSCAN의 파라미터
# eps - 샘플간의 최대 거리
# min_sample = 몇개 이상을 그룹으로 간주 시킴
dbscan = DBSCAN(eps=0.6, min_samples=2)
# DBSCAN은 예측을 바로 시킴
dbscan_data = dbscan.fit_predict(df.loc[:, 'sepal length (cm)':'petal width (cm)'])
# 알아서 분류를 시킴
dbscan_data
array([ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 1,
1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1,
1, 1, 1, 1, -1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 3, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
dtype=int64)
04 군집화 평가 - 실루엣 스코어
- 클러스터링의 품질을 정량적으로 평가해주는 지표
- 1 - 품질이 좋음
0 - 품질이 않좋음 (클러스터링의 의미가 없음)
음수 - 잘못 분류됨
from sklearn.metrics import silhouette_samples, silhouette_score
score = silhouette_score(data_scaled, kmeans.labels_)
score
0.44366157397640527
samples = silhouette_samples(data_scaled, kmeans.labels_)
samples[:5]
array([0.73318987, 0.57783809, 0.68201014, 0.62802187, 0.72693222])- 시각화
def plot_silhouette(X, num_cluesters):
for n_clusters in num_cluesters:
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
# The silhouette coefficient can range from -1, 1 but in this example all
# lie within [-0.1, 1]
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = KMeans(n_clusters=n_clusters, random_state=10)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhouette score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors, edgecolor='k')
# Labeling the clusters
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
s=50, edgecolor='k')
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()
plot_silhouette(data_scaled, [2,3,4,5])- 스캐일화가 된 데이터와 클러스터링 개수를 리스트 형태로 넣으면 된다

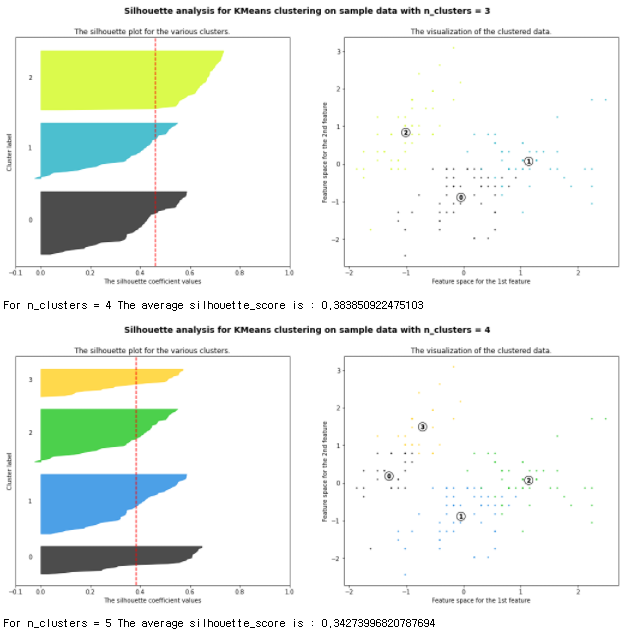

- 비교를 해보면 2개의 군집을 놓을때가 평균이 제일 높게 나온다. 즉 성능이 제일 좋다는 말